Sistema di riferimento¶
 |
Obiettivi: |
Introduzione sui sistemi di riferimento. |
Parole chiave: |
Sistema di riferimento (SR), Proiezione cartografica, Proiezione al volo, Latitudine, Longitudine, Nord, Est |
Panoramica¶
Le proiezioni cartografiche cercano di rappresentare la superficie terrestre o una porzione della stessa su un piano, che sia un foglio di carta o uno schermo. Un sistema di riferimento (SR) definisce, attraverso delle coordinate, come la vostra mappa proiettata nel GIS si collega a posizioni reali sulla terra. La decisione su quale proiezione e quale sistema di rifermento utilizzare dipende dall’estensione della zona in cui volete lavorare, sulle analisi che volete svolgere e spesso sulla disponibilità di dati.
Dettagli sulle proiezioni cartografiche¶
Un metodo tradizionale per rappresentare la forma della Terra è l’uso dei globi. C’è, in ogni caso, un problema con questo approccio. Sebbene i globi conservino la maggior parte della forma della Terra e illustri la configurazione spaiale della geometria dei continenti, ci sono molte difficoltà nel portarli nella tasca di qualcuno. Inoltre, il loro uso è conveniente solo a scale estremamente piccole (per esempio 1:100 milioni)
La maggior parte dei dati per mappe tematiche comunemente utilizzate in applicazioni GIS sono di scala considerevolmente maggiore. Una tipica base dati GIS può avere scale da 1:250000 in su, a seconda del livello di dettaglio. Un globo di questa scala sarebbe costoso da produrre e ancor più da trasportare. Come risultato, i cartografi hanno sviluppato varie tecniche di proiezione cartografica per rappresentare, con ragionevole accuratezza, la superficie sferica della terra in due dimensioni.
Se vista da vicino la terra sembra essere relativamente piatta. Tuttavia, vista dallo spazio, si può notare come la terra sia relativamente sferica. Le mappe, come vedremo nel prossimo argomento sulla produzione cartografica, sono rappresentazioni della realtà. Esse sono progettate per rappresentare non solo degli oggetti territoriali, ma anche la relativa forma e disposizione spaziale. Ogni proiezione cartografica ha i suoi vantaggi e svantaggi. La miglior proiezione per una certa mappa dipende dalla sua scala e dai fini per cui essa sarà utilizzata. Una proiezione può ad esempio avere distorsioni inaccettabili se utilizzata per mappare l’intero continente africano, ma può essere una scelta eccellente per una mappa a grande scala (dettagliata) del vostro paese. Le proprietà di una proiezione cartografica possono influenzare alcune delle caratteristiche di design della mappa. Certe proiezioni sono valide per piccole aree, certe lo sono per descrivere zone con una grande estensione Est-Ovest, e certe altre sono le migliori per la descrizione di aree con una notevole estensione nord-sud.
Le tre famiglie di proiezioni cartografiche¶
Il processo di sviluppo di una proiezione cartografica può essere immaginato mettendo una fonte luminosa puntiforme all’interno di un globo trasparente su cui sono posizionate delle aree geografiche opache. I contorni di queste sono proiettati dalla luce su un pezzo di carta piatto, bidimensionale. Si possono ottenere diversi metodi di proiezione, circondando il globo con un cilindro, con un cono, o anche tramite una superficie piatta. Ciascuno di questi metodi genera quella che viene definita una famiglia di proiezioni cartografiche. Vi è così una famiglia di proiezioni planari, una famiglia di proiezioni cilindriche, e un’altro insieme delle proiezioni coniche (vedi figure_projection_families)
Figure Projection Families 1:
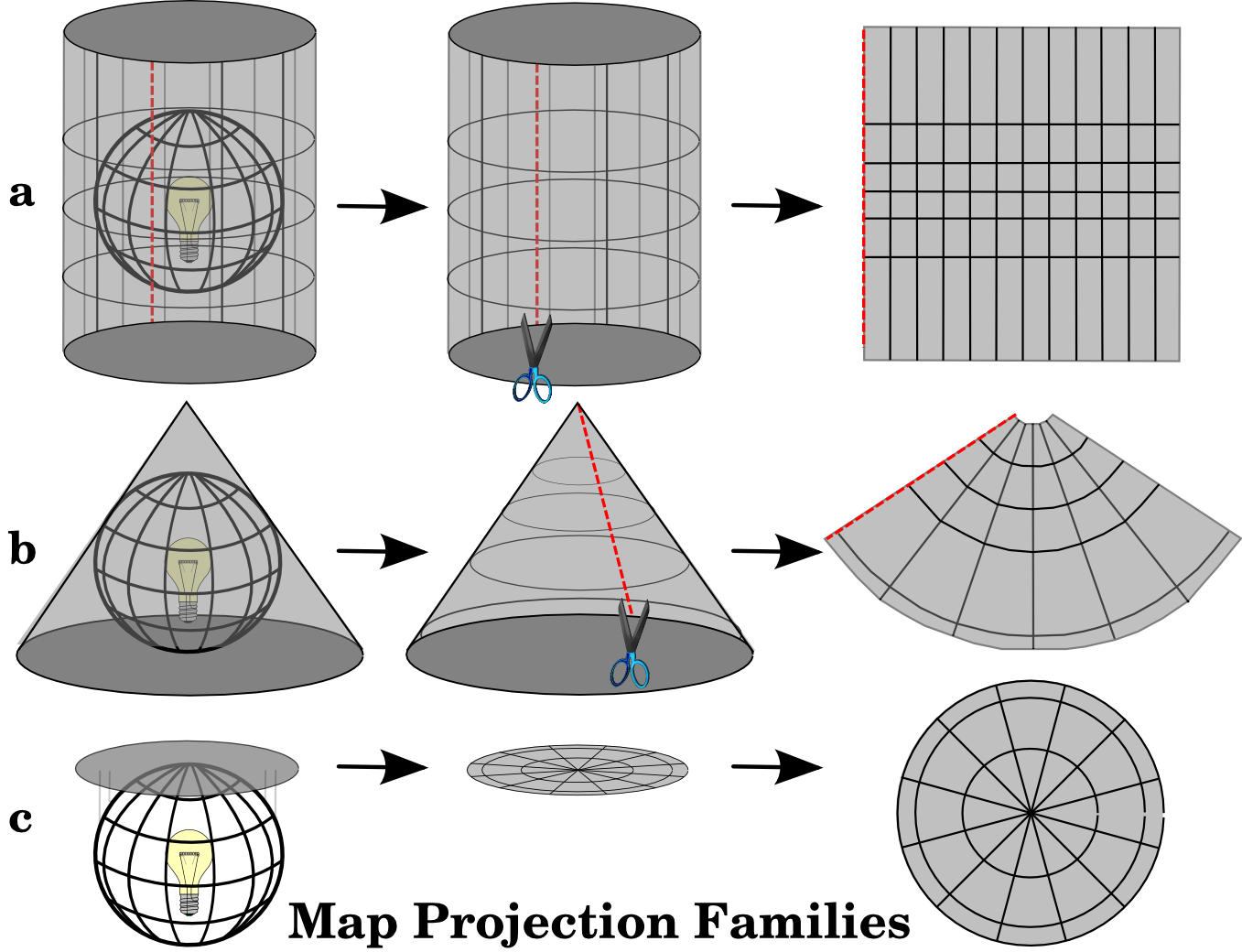
Le tre famiglie di proiezioni cartografiche. Possono essere rappresentate da a) proiezioni cilindriche, b) proiezioni coniche o c) proiezioni piane.
Naturalmente oggi il processo di proiezione della terra su un pezzo di carta è eseguito seguendo i principi matematici della geometria e della trigonometria. Questi processi ricreano la proiezione fisica della luce attraverso il globo trasparente.
Precisione delle proiezioni cartografiche¶
Le proiezioni cartografiche non sono mai delle rappresentazioni esatte della sfericità terrestre. Ogni mappa, a seguito del processo di proiezione cartografico, mostra delle distorsioni per la conformità angolare, di distanza o di superficie. Una proiezione cartografica può combinare alcune di queste caratteristiche, o può essere un compromesso che distorce, entro un limite accettabile, tutte le proprietà di corrispondenza di superficie, distanza e posizionamento angolare. Esempi di proiezioni “compromesso” sono la Proiezione di Winkel-Tripel e la proiezione di Robinson (vedi figure_robinson_projection), spesso utilizzate per le mappe dell’intero globo terrestre.
Figure Robinson Projection 1:
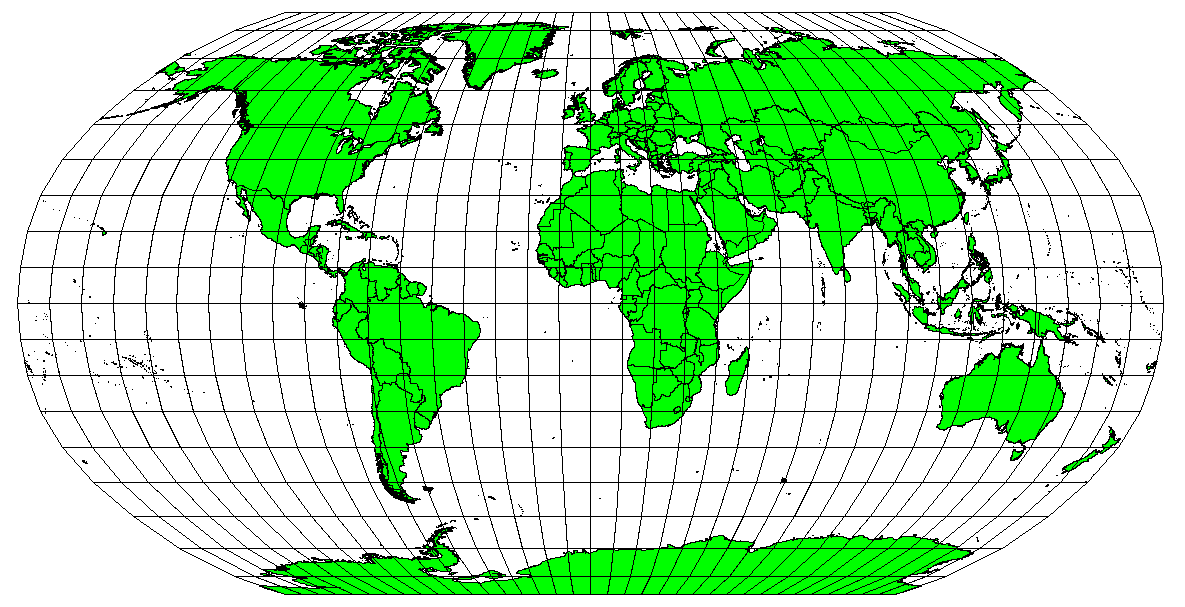
La proiezione di Robinson è un compromesso accettabile per le distorsioni di superficie, conformità angolare e di distanza.
Di solito è impossibile mantenere tutte le caratteristiche allo stesso tempo in una proiezione. Ciò significa che qualora si desideri effettuare operazioni analitiche accurate, sarà necessario utilizzare una proiezione cartografica che fornisca le migliori caratteristiche utili ai processi di analisi. Ad esempio, se vi è la necessità di misurare con precisione le distanze tra oggetti sulla mappa, bisognerà cercar di utilizzare una proiezione cartografica che fornisca un’elevata precisione sulle distanze.
Proiezioni cartografiche isogone o conformi¶
Lavorando a scala di pianeta, le direzioni principali sulla rosa dei venti (Nord, Est, Sud e Ovest) avranno tra di loro una distanza angolare sempre pari a 90 gradi. In altre parole, l’Est sarà sempre ad un angolo di 90 gradi rispetto al nord. Si possono mantene delle proprietà angolari corrette anche in una una proiezione cartografica. Una proiezione cartografica che mantiene le proprietà di conformità angolare è definita conforme o proiezione ortomorfica.
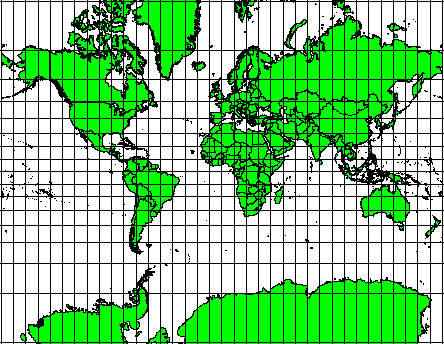
Questo tipo di proiezioni è usato quando è importante la conservazione delle relazioni angolari*. Tali proiezioni sono comunemente utilizzate per le attività di navigazione o meteorologiche. È importante ricordare che per grandi aree è difficile il mantenimento di angoli veri su una mappa e che tale sistema di proiezione dovrebbe essere eseguito solo per piccole porzioni della terra. La proiezione conforme provoca la distorsione delle aree, il che significa che se le misure delle superfici sono fatte su mappa proiettata, esse non saranno corrette. Più grande è l’area, meno accurate saranno le misure della sua superficie. La **proiezione di Mercatore (come mostrato nella figure_mercator_projection) e la Proiezione conica conforme di Lambert sono degli esempi. Il servizio geologico USA utilizza una proiezione conforme per molte delle sue mappe topografiche.
Figure Mercator Projection 1:
Proiezioni cartografiche equidistanti¶
Se il vostro obiettivo nel proiettare una mappa è quello di misurare con precisione le distanze, sarà necessario selezionare una proiezione che sia stata progettata per preservare le distanze. Tali proiezioni, chiamate proiezioni equidistanti, richiedono che la scala della mappa sia mantenuta costante. Una mappa è equidistante qualora rappresenti correttamente le distanze dal centro della proiezione a qualsiasi altro punto sulla mappa. Le Proiezioni equidistanti mantengono distanze corrette dal centro della proiezione o lungo determinate direzioni. Queste proiezioni sono utilizzate per mappature radio, per quelle sismiche e per la navigazione. La proiezione Plate Carrée cilindrica equidistante (vedi figure_plate_caree_projection) e la proiezione equirettangolare sono due buoni esempi di proiezioni equidistanti. La proiezione azimutale equidistante è la proiezione utilizzata per l’emblema delle Nazioni Unite (vedi figure_azimuthal_equidistant_projection).
Figure Plate Carree Projection 1:
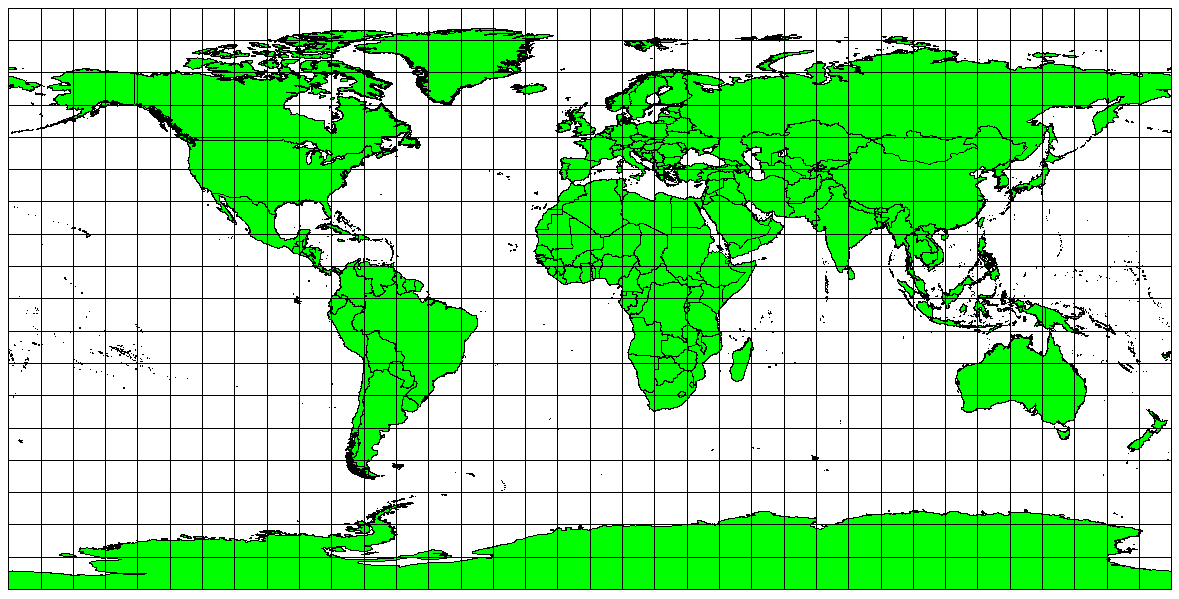
La proiezione cilindrica equidistante Plate Carrée, ad esempio, viene adottata qualora sia importante la misura esatta delle distanze.
Figure Azimuthal Equidistant Projection 1:
Proiezioni equivalenti - mantenimento delle aree¶
Quando una mappa ritrae aree sull’intera mappa, in modo che tutte le aree mappate abbiano lo stesso rapporto proporzionale alle aree rappresentate sulla superficie terrestre, la mappa è un mappa equiareale. In pratica, riferimenti generali e mappe educative spesso richiedono l’uso di proiezioni equiareali. Come suggerisce il nome, queste mappe sono utilizzate quando vengono fatti prevalentemente calcoli sulle aree. Se, per esempio, si sta cercando di analizzare una particolare area nella vostra città per scoprire se è abbastanza grande per un nuovo centro commerciale, proiezioni equiareali saranno la scelta migliore. Da un lato, maggiore è l’area che si sta analizzando più precise saranno le vostre misure areali, nel caso si utilizzi una proiezione equiareale piuttosto che un altro tipo. D’altra parte, una proiezione equiareale fornirà distorsioni ** di conformità angolare ** quando si gestiscono grandi aree. Le aree piccole saranno molto meno inclini ad avere distorsioni angolari quando si utilizza una proiezione equiareale. ** Alber equal area**, Lambert equal area e ** Proiezione ilindrica di Mollweide Equal Area** (mostrati nella figura figure_mollweide_equal_area_projection) sono proiezioni equiareali che si incontrano spesso nel lavoro GIS.
Figure Mollweide Equal Area Projection 1:
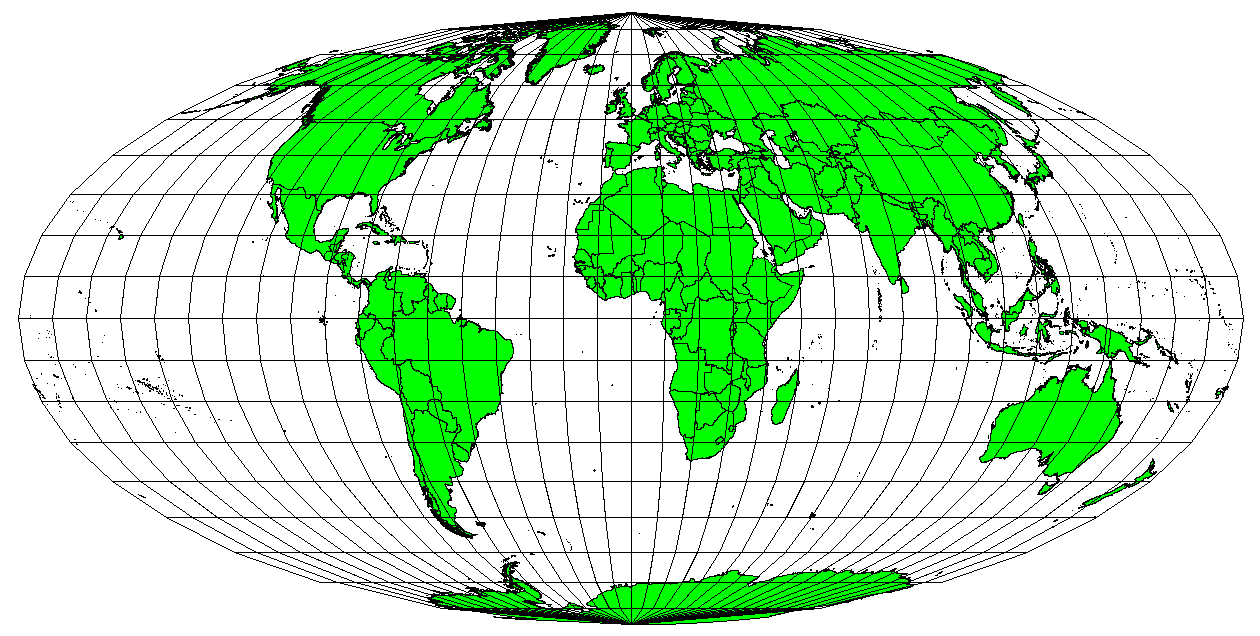
La Proiezione Cilindrica Equiareale Mollweide, ad esempio, assicura che tutte le aree cartografate abbiano la stessa relazione proporzionale con le relative aree sulla superficie terrestre.
Ricorda che le proiezioni sono un argomento molto complesso. Esistono centinaia di proiezioni diverse al mondo ed ognuna cerca di rappresentare una certa porzione di superficie terrestre, quanto più fedelmente possibile su una superficie piatta. In realtà la scelta della proiezione da usare dipende da te. Molte nazioni hanno comunemente usato proiezioni e quando vengo scambiati dei dati le persone seguiranno la tendenza nazionale.
Sistema di riferimento (SR) nel dettaglio¶
With the help of coordinate reference systems (CRS) every place on the earth can be specified by a set of three numbers, called coordinates. In general CRS can be divided into projected coordinate reference systems (also called Cartesian or rectangular coordinate reference systems) and geographic coordinate reference systems.
Sistemi Coordinate Geografiche¶
L’utilizzo dei Sistemi di Riferimento è molto comune. Essi usano i gradi di latitudine e longitudine per descrivere una posizione sulla superficie terrestre. Il più noto è quello chiamato WGS 84.
Lines of latitude run parallel to the equator and divide the earth into 180 equally spaced sections from North to South (or South to North). The reference line for latitude is the equator and each hemisphere is divided into ninety sections, each representing one degree of latitude. In the northern hemisphere, degrees of latitude are measured from zero at the equator to ninety at the north pole. In the southern hemisphere, degrees of latitude are measured from zero at the equator to ninety degrees at the south pole. To simplify the digitisation of maps, degrees of latitude in the southern hemisphere are often assigned negative values (0 to -90°). Wherever you are on the earth’s surface, the distance between the lines of latitude is the same (60 nautical miles). See figure_geographic_crs for a pictorial view.
Figure Geographic CRS 1:
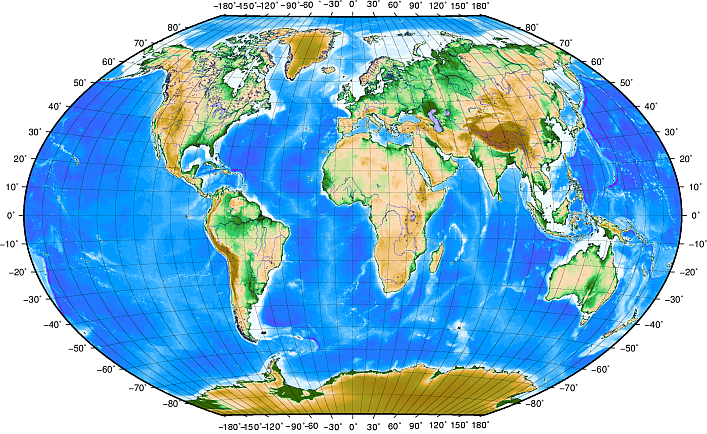
Geographic coordinate system with lines of latitude parallel to the equator and lines of longitude with the prime meridian through Greenwich.
Lines of longitude, on the other hand, do not stand up so well to the standard of uniformity. Lines of longitude run perpendicular to the equator and converge at the poles. The reference line for longitude (the prime meridian) runs from the North pole to the South pole through Greenwich, England. Subsequent lines of longitude are measured from zero to 180 degrees East or West of the prime meridian. Note that values West of the prime meridian are assigned negative values for use in digital mapping applications. See figure_geographic_crs for a pictorial view.
At the equator, and only at the equator, the distance represented by one line of longitude is equal to the distance represented by one degree of latitude. As you move towards the poles, the distance between lines of longitude becomes progressively less, until, at the exact location of the pole, all 360° of longitude are represented by a single point that you could put your finger on (you probably would want to wear gloves though). Using the geographic coordinate system, we have a grid of lines dividing the earth into squares that cover approximately 12363.365 square kilometres at the equator — a good start, but not very useful for determining the location of anything within that square.
To be truly useful, a map grid must be divided into small enough sections so that they can be used to describe (with an acceptable level of accuracy) the location of a point on the map. To accomplish this, degrees are divided into minutes (') and seconds ("). There are sixty minutes in a degree, and sixty seconds in a minute (3600 seconds in a degree). So, at the equator, one second of latitude or longitude = 30.87624 meters.
Sistema di Riferimento proiettato¶
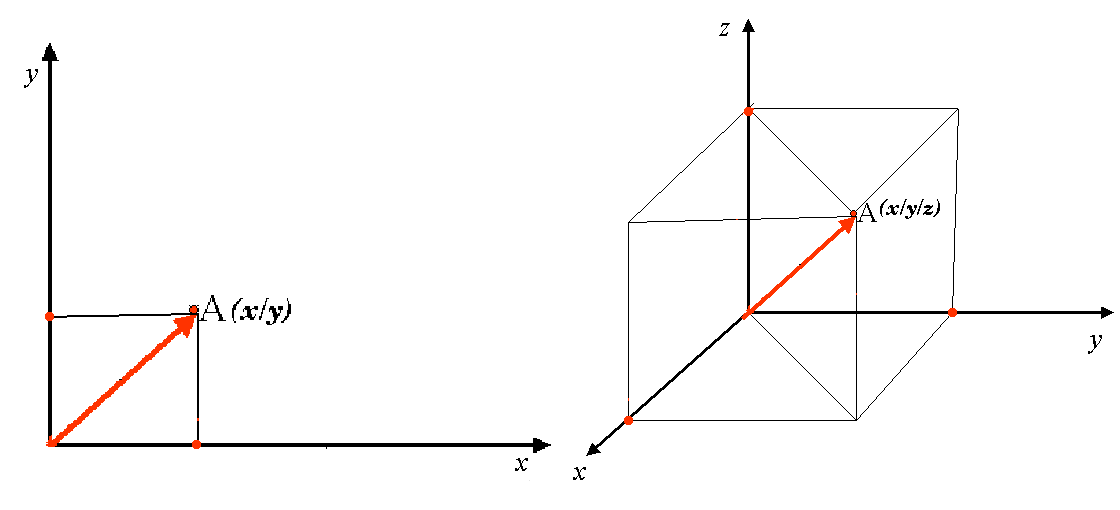
A two-dimensional coordinate reference system is commonly defined by two axes. At right angles to each other, they form a so called XY-plane (see figure_projected_crs on the left side). The horizontal axis is normally labelled X, and the vertical axis is normally labelled Y. In a three-dimensional coordinate reference system, another axis, normally labelled Z, is added. It is also at right angles to the X and Y axes. The Z axis provides the third dimension of space (see figure_projected_crs on the right side). Every point that is expressed in spherical coordinates can be expressed as an X Y Z coordinate.
Figure Projected CRS 1:
A projected coordinate reference system in the southern hemisphere (south of the equator) normally has its origin on the equator at a specific Longitude. This means that the Y-values increase southwards and the X-values increase to the West. In the northern hemisphere (north of the equator) the origin is also the equator at a specific Longitude. However, now the Y-values increase northwards and the X-values increase to the East. In the following section, we describe a projected coordinate reference system, called Universal Transverse Mercator (UTM) often used for South Africa.
SR Universal Transverse Mercator (UTM) nel dettaglio¶
The Universal Transverse Mercator (UTM) coordinate reference system has its origin on the equator at a specific Longitude. Now the Y-values increase southwards and the X-values increase to the West. The UTM CRS is a global map projection. This means, it is generally used all over the world. But as already described in the section ‘accuracy of map projections’ above, the larger the area (for example South Africa) the more distortion of angular conformity, distance and area occur. To avoid too much distortion, the world is divided into 60 equal zones that are all 6 degrees wide in longitude from East to West. The UTM zones are numbered 1 to 60, starting at the international date line (zone 1 at 180 degrees West longitude) and progressing East back to the international date line (zone 60 at 180 degrees East longitude) as shown in figure_utm_zones.
Figure UTM Zones 1:
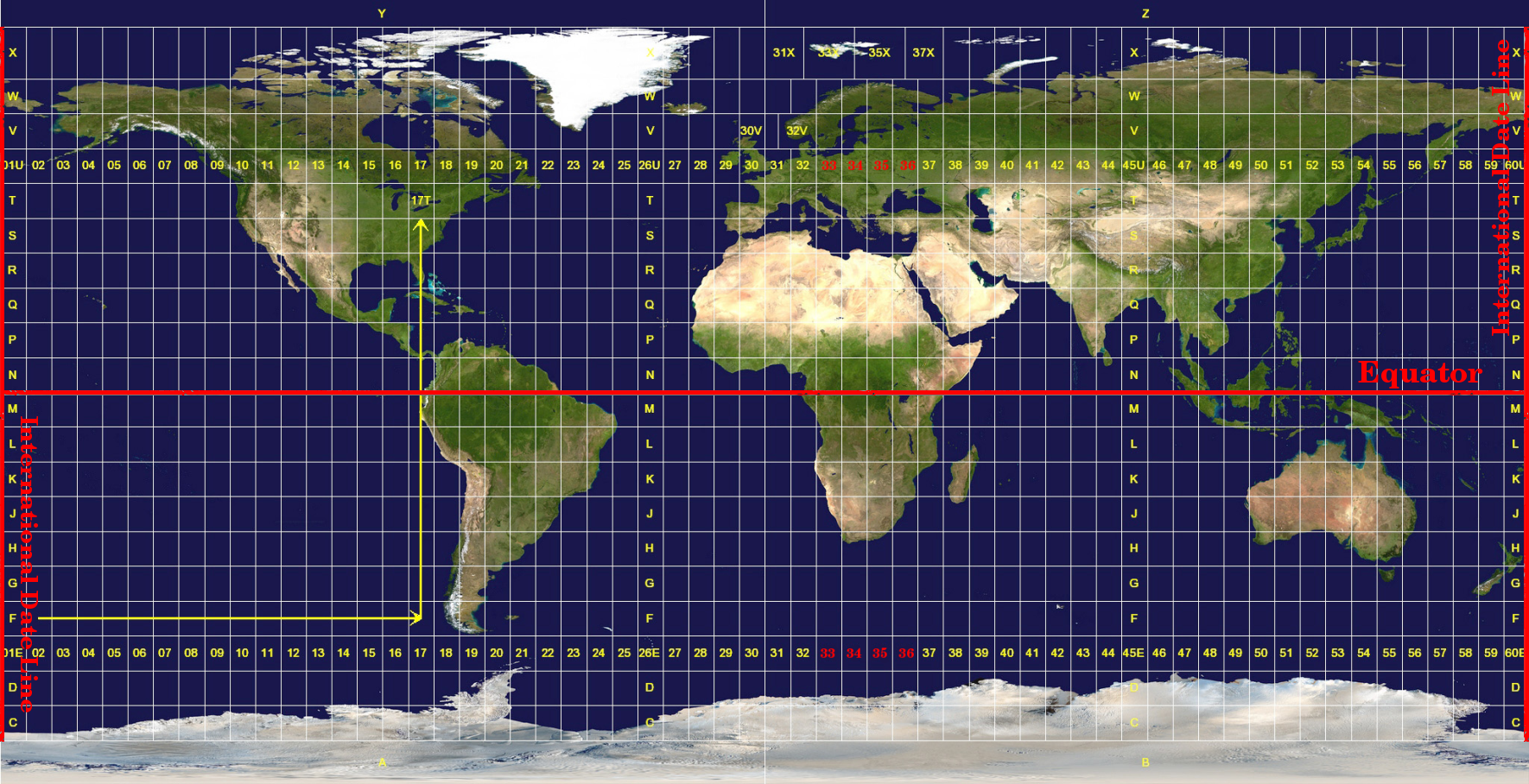
The Universal Transverse Mercator zones. For South Africa UTM zones 33S, 34S, 35S, and 36S are used.
As you can see in figure_utm_zones and figure_utm_for_sa, South Africa is covered by four UTM zones to minimize distortion. The zones are called UTM 33S, UTM 34S, UTM 35S and UTM 36S. The S after the zone means that the UTM zones are located south of the equator.
Figure UTM for South Africa 1:
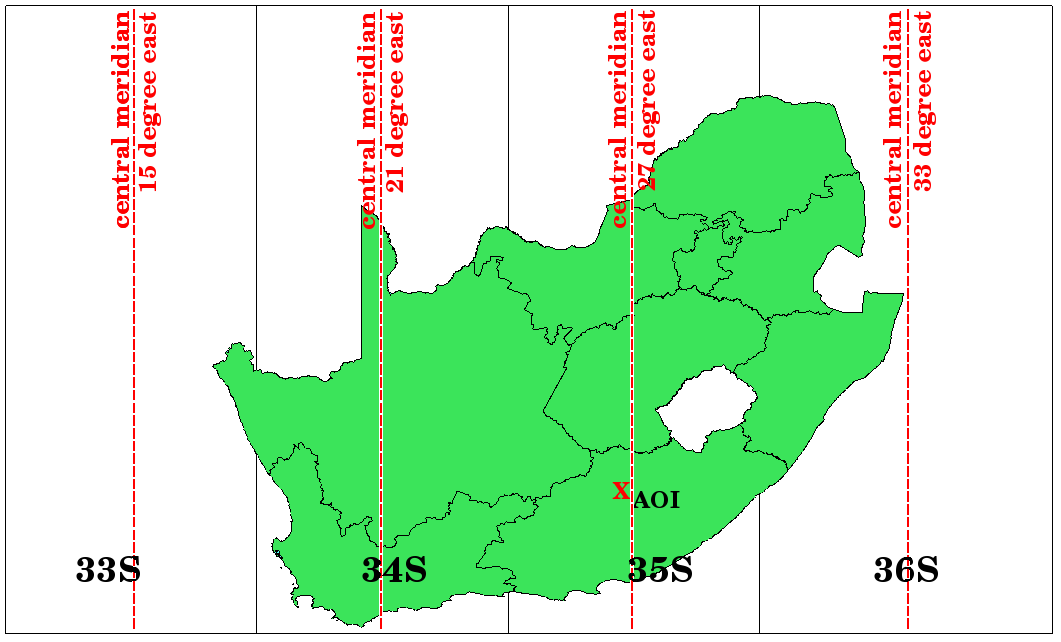
UTM zones 33S, 34S, 35S, and 36S with their central longitudes (meridians) used to project South Africa with high accuracy. The red cross shows an Area of Interest (AOI).
Say, for example, that we want to define a two-dimensional coordinate within the Area of Interest (AOI) marked with a red cross in figure_utm_for_sa. You can see, that the area is located within the UTM zone 35S. This means, to minimize distortion and to get accurate analysis results, we should use UTM zone 35S as the coordinate reference system.
The position of a coordinate in UTM south of the equator must be indicated with the zone number (35) and with its northing (y) value and easting (x) value in meters. The northing value is the distance of the position from the equator in meters. The easting value is the distance from the central meridian (longitude) of the used UTM zone. For UTM zone 35S it is 27 degrees East as shown in figure_utm_for_sa. Furthermore, because we are south of the equator and negative values are not allowed in the UTM coordinate reference system, we have to add a so called false northing value of 10,000,000 m to the northing (y) value and a false easting value of 500,000 m to the easting (x) value. This sounds difficult, so, we will do an example that shows you how to find the correct UTM 35S coordinate for the Area of Interest.
The northing (y) value¶
The place we are looking for is 3,550,000 meters south of the equator, so the northing (y) value gets a negative sign and is -3,550,000 m. According to the UTM definitions we have to add a false northing value of 10,000,000 m. This means the northing (y) value of our coordinate is 6,450,000 m (-3,550,000 m + 10,000,000 m).
The easting (x) value¶
First we have to find the central meridian (longitude) for the UTM zone 35S. As we can see in figure_utm_for_sa it is 27 degrees East. The place we are looking for is 85,000 meters West from the central meridian. Just like the northing value, the easting (x) value gets a negative sign, giving a result of -85,000 m. According to the UTM definitions we have to add a false easting value of 500,000 m. This means the easting (x) value of our coordinate is 415,000 m (-85,000 m + 500,000 m). Finally, we have to add the zone number to the easting value to get the correct value.
As a result, the coordinate for our Point of Interest, projected in UTM zone 35S would be written as: 35 415,000 m E / 6,450,000 m N. In some GIS, when the correct UTM zone 35S is defined and the units are set to meters within the system, the coordinate could also simply appear as 415,000 6,450,000.
Riproiezione al volo¶
As you can probably imagine, there might be a situation where the data you want to use in a GIS are projected in different coordinate reference systems. For example, you might get a vector layer showing the boundaries of South Africa projected in UTM 35S and another vector layer with point information about rainfall provided in the geographic coordinate system WGS 84. In GIS these two vector layers are placed in totally different areas of the map window, because they have different projections.
Per risolvere questo problema molti GIS includono funzionalità chiamate riproiezione al volo. Questo significa che puoi definire una certa proiezione all’avvio del GIS e tutti i layer che caricherai verranno automaticamente visualizzati nella proiezione da te definita qualunque sia il loro sistema di riferimento delle coordinate. Questa funzionalità permette di sovrapporre layer nella finestra di mappa del tuo GIS, anche nel caso questi abbiano differenti Sistemi di Riferimento.
Problemi comuni / cose di cui essere consapevoli¶
The topic map projection is very complex and even professionals who have studied geography, geodetics or any other GIS related science, often have problems with the correct definition of map projections and coordinate reference systems. Usually when you work with GIS, you already have projected data to start with. In most cases these data will be projected in a certain CRS, so you don’t have to create a new CRS or even re project the data from one CRS to another. That said, it is always useful to have an idea about what map projection and CRS means.
Cosa abbiamo imparato?¶
Cerchiamo di riassumere gli argomenti che abbiamo affrontato in questo foglio di lavoro:
Le ** Proiezioni Mappa ** ritraggono la superficie della terra su un pezzo di carta piano o sullo schermo del computer, entrambe bidimensionali.
Esistono delle proiezioni di mappa globali, ma la maggior parte sono state create ed ottimizzate per piccole aree della superficie trerrestre.
Le Proiezioni di Mappa non sono mai rappresentazioni assolutamente accurate della terra sferica . Essee mostrano distorsioni **di conformità angolae, di distanza e di area zona . ** È impossibile conservare tutte queste caratteristiche insieme in una proiezione.
Un Sistema di Riferimento (SR) definisce, insieme alle coordinate, come una mappa bidimensionale proiettata è in relazine con la localizzazione reale sulla superfice terrestre.
Esistono due diversi tipi di Sistemi di Riferimento: Sistemi di Riferimento Geografici e Sistemi di Riferimento Proiettati.
La proiezione **al volo++ è una funzionalità GIS che permette di sovrpporre tra loro layer anche se proiettati in diversi Sistemi di Riferimento delle coordinate
Adesso prova tu!¶
Ecco alcune idee per provare con i vostri studenti:
- Start QGIS and load two layers of the same area but with different projections
and let your pupils find the coordinates of several places on the two layers.
You can show them that it is not possible to overlay the two layers. Then define
the coordinate reference system as Geographic/WGS 84 inside the
Project Properties dialog and activate the checkbox
 Enable on-the-fly CRS transformation. Load the two layers of the
same area again and let your pupils see how on-the-fly projection works.
Enable on-the-fly CRS transformation. Load the two layers of the
same area again and let your pupils see how on-the-fly projection works. - You can open the Project Properties dialog in QGIS and show your pupils the many different Coordinate Reference Systems so they get an idea of the complexity of this topic. With ‘on-the-fly’ CRS transformation enabled you can select different CRS to display the same layer in different projections.
Qualcosa su cui pensare¶
If you don’t have a computer available, you can show your pupils the principles of the three map projection families. Get a globe and paper and demonstrate how cylindrical, conical and planar projections work in general. With the help of a transparency sheet you can draw a two-dimensional coordinate reference system showing X axes and Y axes. Then, let your pupils define coordinates (x and y values) for different places.
Ulteriori link¶
Libri:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. Terza edizione. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. Terza edizione. Wiley. ISBN: 9814126195
- Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X
Siti web:
- http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html
- http://geology.isu.edu/geostac/Field_Exercise/topomaps/index.htm
La Guida dell’utente di QGIS contiene informazioni maggiormente dettagliate per lavorare con le proiezioni di mappa in QGIS.
Cosa viene adesso?¶
Nella prossima sezione andremo a vedere in modo più approfondito alla Produzione di Mappe