17.15. Découpage et fusion de couches raster¶
Note
Dans cette leçon, nous verrons un autre exemple de préparation de données spatiales, pour continuer à utiliser des géoalgorithmes dans des scénarios du monde réel.
Pour cette leçon, nous allons calculer une couche de pente pour une zone entourant une zone de ville, qui est donnée dans une couche vecteur avec un seul polygone. Le MNE de base est divisé en deux couches raster qui, ensemble, couvrent une zone beaucoup plus grande que celle autour de la ville avec laquelle nous voulons travailler. Si vous ouvrez le projet correspondant à cette leçon, vous verrez quelque chose comme ça.

Ces couches ont deux problèmes :
Elles couvrent une aire qui est trop grande pour ce que l’on veut (nous nous intéressons à une plus petite région autour du centre ville)
Elles sont dans deux fichiers différents (les limites de la ville tombent dans une seule couche raster, mais, comme cela a été dit, nous voulons des zones supplémentaires autour d’elle).
Ces deux problèmes sont facilement résolvables avec les géoalgorithmes appropriés.
Premièrement, nous créons un rectangle définissant la zone que nous voulons. Pour faire cela, nous créons une couche contenant la boîte englobante de la couche avec les limites de la zone de la ville, et ensuite nous lui mettons un tampon, afin d’obtenir une couche raster qui couvre un peu plus que le strict nécessaire.
Pour calculer la boîte englobante, nous pouvons utiliser l’algorithme Créer un polygone à partir de l’emprise de la couche.
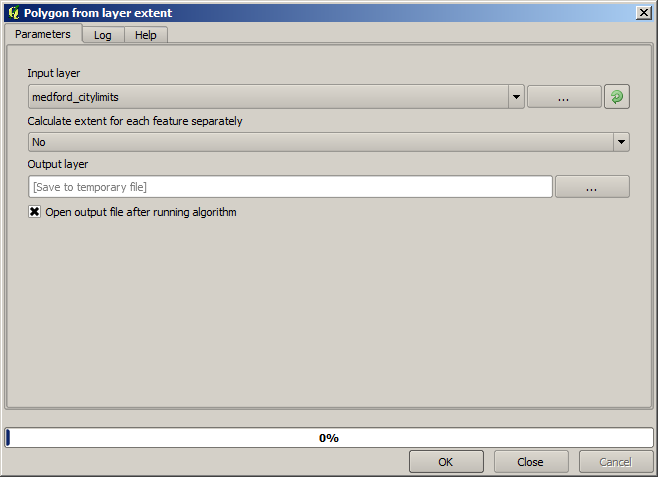
Pour lui mettre un tampon, nous utilisons l’algorithme Tampon à distance fixe, avec les valeurs de paramètres suivantes.
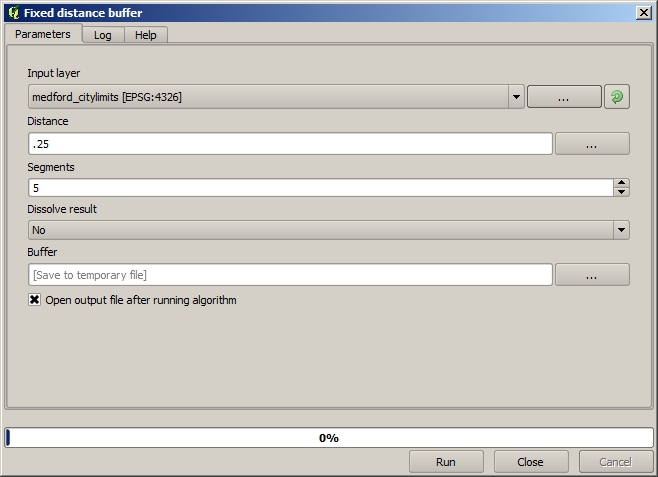
Voici la boîte englobante de résultat obtenue en utilisant les paramètres montrés au-dessus.

C’est une boîte ronde, mais nous pouvons facilement obtenir la boîte équivalente avec des angles droits, en lançant pour elle l’algorithme Créer un polygone à partir de l’emprise de la couche. Nous pourrions avoir fait un tampon sur les limites de la ville d’abord, et ensuite calculer l’emprise du rectangle, en sauvegardant à chaque étape.

Vous remarquerez que les rasters ont une projection différente que celle du vecteur. Nous devons donc les reprojeter avant de poursuivre, en utilisant l’outil Projection (reprojection).
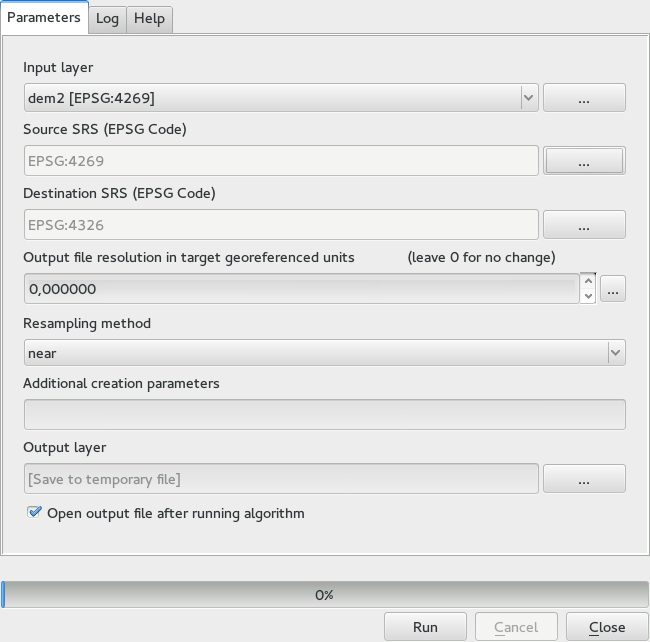
Note
Les versions récentes ont des interfaces plus complexes. Sélectionnez au moins une méthode de compression.
Avec cette couche qui contient la boîte englobante de la couche raster que nous voulons obtenir, nous pouvons recadrer les deux couches rasters, en utilisant l’algorithme Découper une grille avec des polygones.
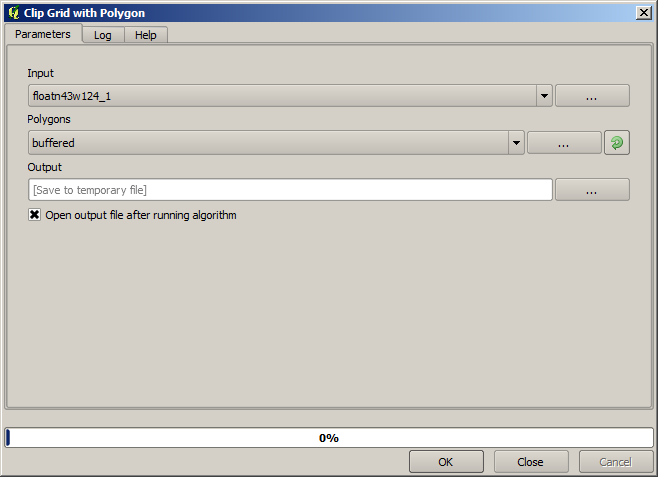
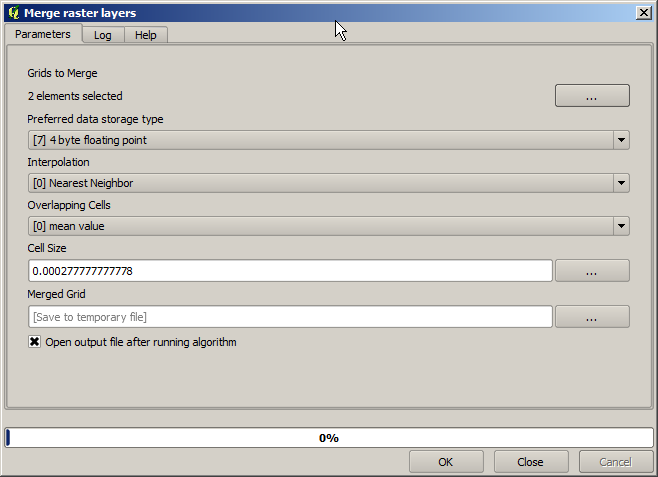
Une fois que les couches ont été recadrées, elles peuvent être fusionnées en utilisant l’algorithme Fusionner de GDAL.
Warning
Le paragraphe suivant est obsolète.
Une taille de cellule est nécessaire pour la couche fusionnée. Nous utiliserons la même que celle des couches d’entrée. Vous n’avez pas besoin de la connaître à l’avance avant d’appeler l’algorithme. Cliquez simplement sur le bouton sur le côté droit du champ de texte et vous obtiendrez une boîte de dialogue pour entrer de petites formules mathématiques, et une liste des valeurs fréquemment utilisées, au milieu d’elles les tailles de cellules et les coordonnées de la boîte de toutes les couches disponibles.
Note
Vous pouvez gagner du temps en fusionnant d’abord et en recadrant ensuite, et vous éviterez d’appeler deux fois l’algorithme de découpage. Cependant, s’il y a plusieurs couches à fusionner et qu’elles ont une assez grande taille, vous finirez avec une grande couche qui pourra être difficile à traiter plus tard. Dans ce cas, vous devriez appeler l’algorithme de découpage plusieurs fois, ce qui peut prendre beaucoup de temps, mais ne vous inquiétez pas, nous verrons bientôt qu’il existe des outils supplémentaires pour automatiser cette opération. Dans cet exemple, nous n’avons que deux couches, donc vous n’aurez pas besoin de vous soucier de cela maintenant.
Avec cela, nous obtenons le MNE final que nous voulons.
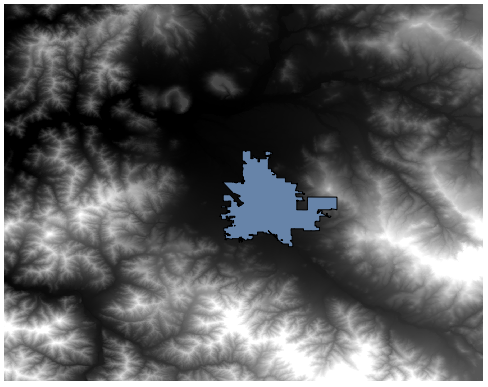
Il est maintenant temps de calculer la couche de pente.
Une couche de pente peut être calculée avec l’algorithme Pente, Aspect, Courbes, mais le MNE obtenu dans la dernière étape n’est pas approprié comme entrée, puisque les valeurs d’élévation sont en mètre mais la taille de cellule n’est pas exprimée en mètre (la couche utilise un SCR avec des coordonnées géographiques). Une reprojection est nécessaire. Pour reprojeter une couche raster, l’algorithme Projection (reprojection) peut encore être utilisé. Nous reprojetons dans un SCR avec des mètres comme unités (par exemple 3857), donc nous pouvons ensuite calculer correctement la pente, avec soit SAGA soit GDAL.
Voici le MNE reprojeté.

Avec ce nouveau MNE, la pente peut maintenant être calculée.
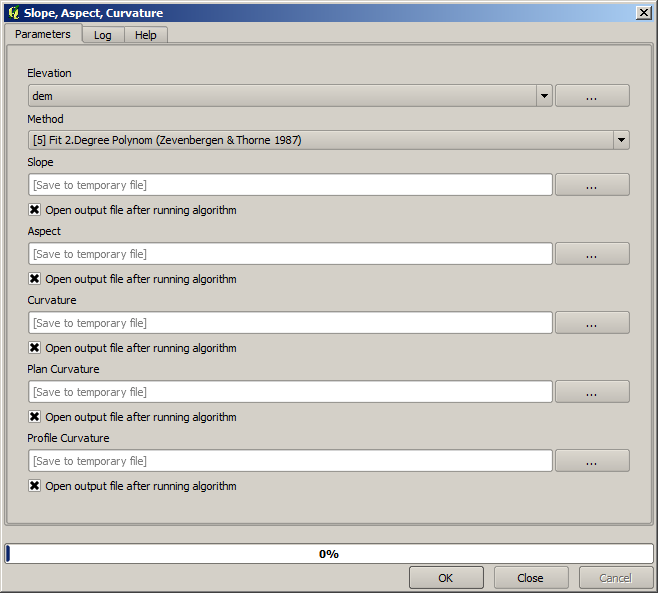
Et voici la couche de pente de résultat.
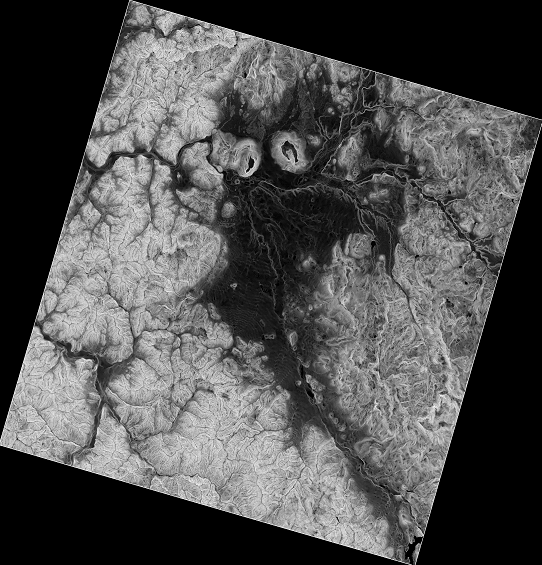
La pente produite par l’algorithme Pente, Aspect, Courbes est exprimée en radian, mais les degrés sont une unité plus pratique et plus commune. L’algorithme Conversions métriques nous aidera à faire la conversion (mais dans le cas où vous ne sauriez pas que cet algorithme existe, vous pourriez utiliser la calculatrice raster que nous avons déjà utilisée).
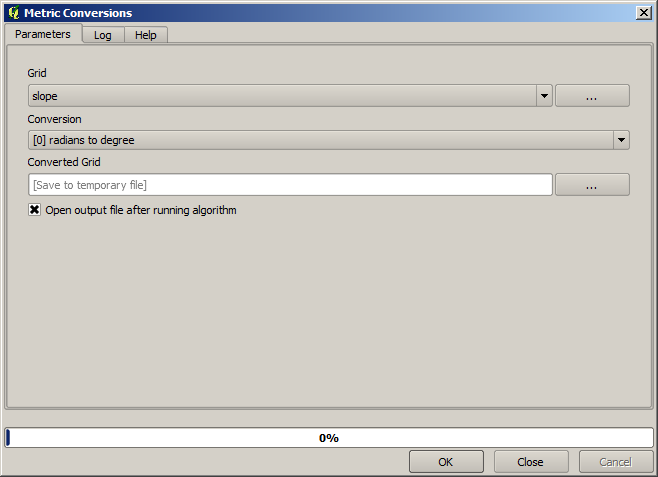
En reprojetant la couche de pente reconvertie avec la Reprojection de couche raster, nous obtenons la couche finale que nous souhaitons.
Warning
todo: Ajouter une image
Les processus de reprojection ont donné la couche finale qui contient des données en dehors de la boîte englobante que nous avons calculée dans une des premières étapes. Cela peut être résolu en la découpant à nouveau, comme nous l’avons fait pour obtenir le MNE de base.